August 2018 Geometry Regents Answers Part 1: Answers with Explanations

The Geometry Regents exam is a critical test for high school students in New York State. It assesses understanding of geometric principles and the ability to apply them in various scenarios. This detailed breakdown will cover August 2018 Geometry Regents Answers Part 1, providing insights and solutions to help you grasp the underlying concepts. In New York, Regents are required for graduation

August 2018 Geometry Regents Answers Part 1: All answers with explanation.

Whatever the exam, the previous year’s questions and their answers to that exam helped us a lot in preparing for our exam. The regents exam schedule for June 2024 has been released and students have started preparing for it. For their preparation, below we have given all the questions and their answers to the 2018 geometry regents exam part 1.

Question 1: Finding the Measure of an Angle

In the diagram below, AEFB || CGD, and GE and GF are drawn.

Given: m∠EFG = 32° and m∠AEG = 137°. Find m∠EGF.

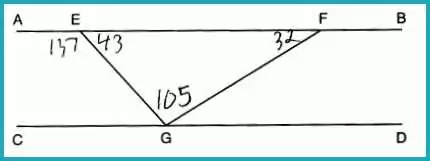
Answer: (4) 105°

To solve this, note that ∠AEG is an exterior angle to triangle EFG. Using the exterior angle theorem:

∠FEG = 180° – 137° = 43°

The sum of angles in triangle EFG = 180°

Thus, ∠EGF = 180° – (43° + 32°) = 105°

Question 2: Relationship Between Triangles

If triangle ABC is mapped onto triangle DEF after a reflection and then onto triangle XYZ after a translation, what is the relationship between triangle ABC and triangle XYZ?

Answer: (1) congruent and similar

Reflections and translations are rigid motions, which preserve the shape and size of the object. Therefore, the triangles remain congruent and similar.

Question 3: 3D Object from Rotating a Triangle

An isosceles right triangle with legs of 6 is rotated about one of its legs to form a three-dimensional object. What is the object?

Answer: (4) cone with a diameter of 12

Rotating a right triangle about one of its legs forms a cone. The radius of the base of the cone is 6, thus the diameter is 12.

Question 4: Reflecting and Rotating a Triangle

In a regular hexagon ABCDEF, AD, BE, and CF intersect at G. What happens when triangle ABG is reflected over BG and rotated 180° about point G?

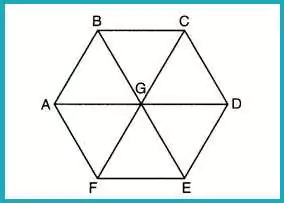
Answer: (1) Triangle FEG

Upon reflection, triangle ABG maps onto BGC, and a subsequent 180° rotation maps it onto FEG.

Question 5: Cross Section of a Cylinder

A right cylinder is cut perpendicular to its base. What is the shape of the cross section?

Answer: (3) rectangle

A perpendicular cut to the base of a cylinder results in a rectangular cross-section.

Question 6: Calculating Springboard Length

Yolanda is making a springboard with 8-inch-tall springs forming a 16.5° angle with the base. What is the length of the springboard, x, to the nearest tenth of an inch?

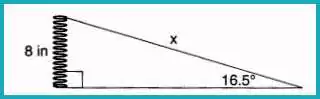
Answer: (4) 28.2

Using the sine function:

sin⁡(16.5°)=8xx=8sin⁡(16.5°)≈28.2\sin(16.5°) = \frac{8}{x} \\ x = \frac{8}{\sin(16.5°)} \approx 28.2sin(16.5°)=x8​x=sin(16.5°)8​≈28.2

Question 7: Length of a Triangle Side

In right triangle ABC with altitude BD drawn to hypotenuse AC, given BD = 4, AD = x – 6, and CD = x, what is the length of the CD?

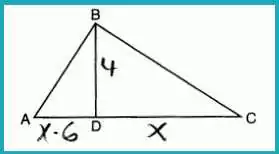
Answer: (3) 8

Using the Right Triangle Altitude Theorem:

BD2=AD×CD42=(x−6)×x16=x2−6xx2−6x−16=0(x−8)(x+2)=0x=8 (discarding the negative solution)BD^2 = AD \times CD \\ 4^2 = (x – 6) \times x \\ 16 = x^2 – 6x \\ x^2 – 6x – 16 = 0 \\ (x – 8)(x + 2) = 0 \\ x = 8 \text{ (discarding the negative solution)}BD2=AD×CD42=(x−6)×x16=x2−6xx2−6x−16=0(x−8)(x+2)=0x=8 (discarding the negative solution)

Question 8: Perimeter of a Rhombus

Rhombus STAR has vertices S(–1,2), T(2,3), A(3,0), and R(0,–1). What is the perimeter?

Answer: (4) 4 * sqrt(10)

Calculate one side using the distance formula:

Distance=(2−(−1))2+(3−2)2=9+1=10Perimeter=4×10\text{Distance} = \sqrt{(2 – (-1))^2 + (3 – 2)^2} = \sqrt{9 + 1} = \sqrt{10} \\ \text{Perimeter} = 4 \times \sqrt{10}Distance=(2−(−1))2+(3−2)2​=9+1​=10​Perimeter=4×10​

Question 9: Measuring an Angle

In triangles HAR and NTY, angles H and N are right angles, and HAR ~ NTY. If AR = 13 and HR = 12, what is the measure of angle Y?

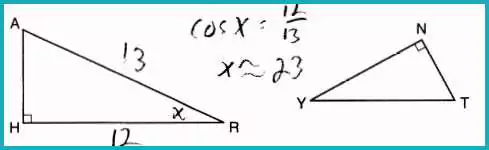
Answer: (1) 23°

Using cosine:

cos⁡R=1213R=cos⁡−1(1213)≈23°\cos R = \frac{12}{13} \\ R = \cos^{-1}\left(\frac{12}{13}\right) \approx 23°cosR=1312​R=cos−1(1312​)≈23°

Question 10: Proving Triangle Congruence

In the diagram below, AKS, NKC, AN, and SC are drawn such that AN = SC. What additional statement is sufficient to prove triangle KAN = triangle KSC by AAS?

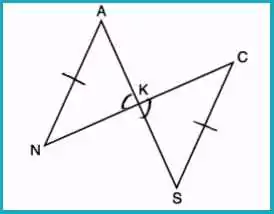
Answer: (4) AN || SC

Parallel lines provide alternate interior angles, leading to sufficient information to use AAS for proving congruency.

Question 11: Equation of a Perpendicular Line

Which equation represents a line perpendicular to y = (2/3)x + 1?

Answer: (1) 3x + 2y = 12

The slope of the perpendicular line is the negative reciprocal of 2/3, which is -3/2. Thus, the equation is 3x + 2y = 12.

Question 12: Length in Proportional Segments

In triangle ABC, points D and E are on sides AB and CB such that DE || AC. Given EB is 3 more than DB, AB = 14, and CD = 21, what is the length of AD?

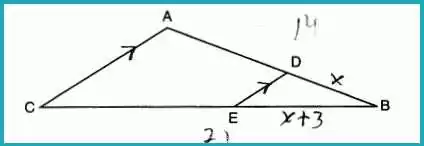
Answer: (2) 8

Set up the proportion:

x14=x+32121x=14x+427x=42x=6AD=14−6=8\frac{x}{14} = \frac{x + 3}{21} \\ 21x = 14x + 42 \\ 7x = 42 \\ x = 6 \\ AD = 14 – 6 = 814x​=21x+3​21x=14x+427x=42x=6AD=14−6=8

Question 13: Properties of a Quadrilateral

Quadrilateral MATH has both pairs of opposite sides congruent and parallel. What is always true about quadrilateral MATH?

Answer: (4) ∠MAT = ∠MHT

This property holds for parallelograms, where opposite angles are congruent.

Question 14: Perimeter of a Circumscribed Quadrilateral

In quadrilateral TAEO circumscribed around circle D, midpoint R of TA and HO = PE, given AP = 10 and EO = 12, what is the perimeter?

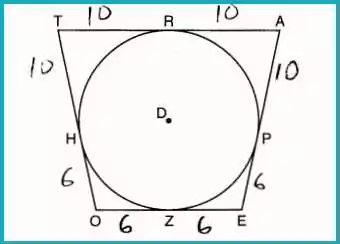
Answer: (2) 64

$$AP=AR=10\text{(R is midpoint)}RT=TH=10HO=PE=6\text{Perimeter}=4\times 10+4\times 6=64$$

Question 15: Coordinates of a Point on a Line Segment

The endpoints of directed line segment ABC are A(-8,7) and C(7,-13). If AB

= 3:2, what are the coordinates of B?

Answer: (1) (1, -5)

Calculate:

x coordinate=−8+35×15=1y coordinate=7+35×(−20)=−5x \text{ coordinate} = -8 + \frac{3}{5} \times 15 = 1 \\ y \text{ coordinate} = 7 + \frac{3}{5} \times (-20) = -5x coordinate=−8+53​×15=1y coordinate=7+53​×(−20)=−5

Question 16: Length of DE in Proportional Triangles

In triangle ABC, points D and E are on sides AB and BC such that DE || AC, with AD

= 3:5. If DB = 6.3 and AC = 9.4, what is the length of DE?

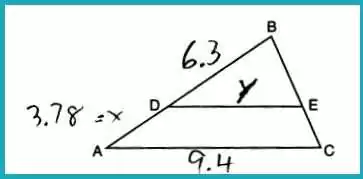
Answer: (3) 5.9

Using proportions:

ACDE=85DE=5×9.48=5.875≈5.9\frac{AC}{DE} = \frac{8}{5} \\ DE = \frac{5 \times 9.4}{8} = 5.875 \approx 5.9DEAC​=58​DE=85×9.4​=5.875≈5.9

Question 17: Transformation of a Rectangle

Rectangle ABCD has vertices A(7,1), B(9,3), C(3,9), and D(1,7). Which transformation will not carry the rectangle onto itself?

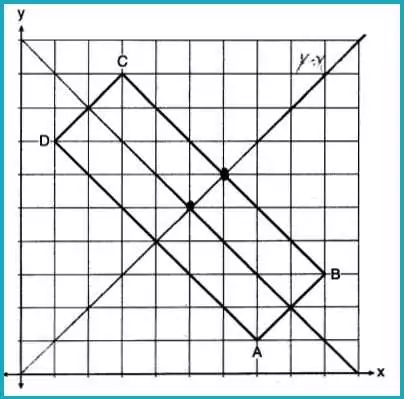
Answer: (3) a rotation of 180° about the point (6,6)

The center of the rectangle is (5, 5), not (6, 6). Thus, the image would not coincide with the original.

Question 18: Area of a Circle Sector

A circle with a diameter of 10 cm has a central angle of 30°. What is the area of the sector?

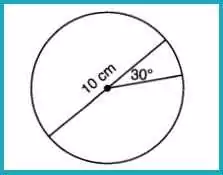
Answer: (2) 6.5

Radius = 5 cm, and the sector’s area is:

30°360°×π×52=112×25π≈6.54≈6.5\frac{30°}{360°} \times \pi \times 5^2 = \frac{1}{12} \times 25\pi \approx 6.54 \approx 6.5360°30°​×π×52=121​×25π≈6.54≈6.5

Question 19: Proving Congruence Using Transformation

Which transformation maps (x,y) onto (x + 3, -y + 4)?

Answer: (3) 180° rotation and translation 3 units right and 4 units up

First perform the rotation (x,y) -> (-x,-y) then translate (x + 3, -y + 4).

Question 20: Finding a Scale Factor

The transformation Dk maps point P(x, y) onto P'(kx, ky). If P(4, 8) maps to P'(8, 16), what is the value of k?

Answer: (4) 2

Scale factor k:

$$8=4k16=8kk=2$$

Question 21: Equation of a Line in Perpendicular Bisector

Line segment AB has endpoints A(-3, -1) and B(5, 3). What is the equation of the line that is the perpendicular bisector of AB?

Answer: (4) y = -2x + 6

Midpoint:

(−3+52,−1+32)=(1,1)\left(\frac{-3 + 5}{2}, \frac{-1 + 3}{2}\right) = (1, 1)(2−3+5​,2−1+3​)=(1,1)Slope of AB:

3−(−1)5−(−3)=48=12\frac{3 – (-1)}{5 – (-3)} = \frac{4}{8} = \frac{1}{2}5−(−3)3−(−1)​=84​=21​Slope of perpendicular bisector:

$$-2Equationofthelinethrough(1,1):\text{[}y-1=-2(x-1)y=-2x+2+1=-2x+6$$

Question 22: Calculating a Perimeter of a Regular Polygon

What is the perimeter of a regular polygon with 12 sides, each side having length 3√3?

Answer: (4) 36√3

12×33=36312 \times 3\sqrt{3} = 36\sqrt{3}12×33​=363​

Question 23: Verifying Similar Triangles

Triangles ABC and DEF are similar with AB = 6, AC = 8, DE = 9, and DF = 12. What is the ratio of their areas?

Answer: (2) 9/4

(ABDE)2=(69)2=(23)2=49\left(\frac{AB}{DE}\right)^2 = \left(\frac{6}{9}\right)^2 = \left(\frac{2}{3}\right)^2 = \frac{4}{9}(DEAB​)2=(96​)2=(32​)2=94​

Question 24: Analyzing a Circle

The equation of a circle is (x – 2)^2 + (y – 3)^2 = 25. What is the centre and radius of the circle?

Answer: (2) (2, 3) and 5

Center: (2,3)Radius: 25=5\text{Center: } (2, 3) \\ \text{Radius: } \sqrt{25} = 5Center: (2,3)Radius: 25​=5

(( Reference: All questions have been gathered from the official NYSED website and the answers have been solved and explained by us. For more information, please visit the official NYSED website. ))

Conclusion:

The August 2018 Geometry Regents Exam, Part 1, covers a wide range of topics that test students’ understanding of geometric principles and their application. From calculating angles and perimeters to understanding transformations and proving congruence, these questions are designed to challenge and enhance a student’s problem-solving skills.

By reviewing these answers, students can gain a clearer understanding of the concepts and improve their performance in future exams.